Chapter 4 - Excess Carriers and Relaxation
ECE 4339
Han Q. Le
(copyrighted) U. of Houston
0. Physical constants or frequently used formulas
Overview
1. Excess carriers and quasi-Fermi levels
2. Carrier relaxation-microscopic mechanism
3. Population relaxation
3.1 Population dynamics concept
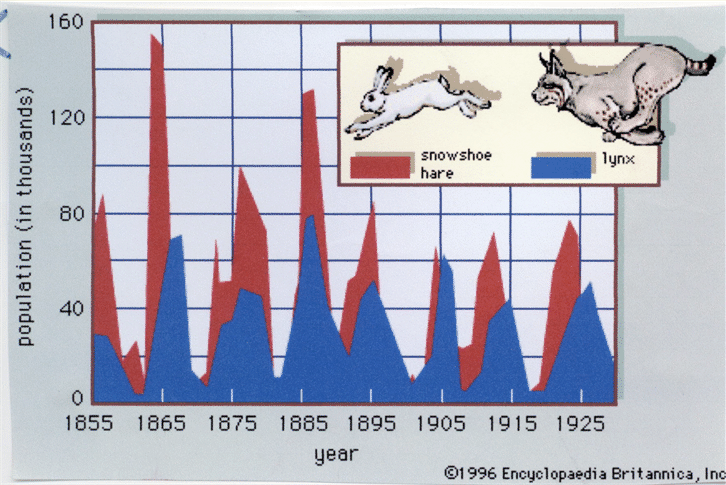
The Lynx and Hare Oscillation Model
This is a famous, simple but powerful model, which was the basis
of a masters thesis at MIT in the 1970s. The student was
supervised by J. W. Forrester himself, and the paper was very well
written and researched. It starts with arctic hares (large
rabbits). The number of hares is given by the level Hares. This
intial number of hares is 5E4 in STELLA which is equal
to 50,000. The Hares population increases by Hare
Births, and decreases by Hare Deaths. The model runs over a matter
of 40 years.
source:
http://www.sonoma.edu/users/n/Norwick/Classes/MODELING/How%20to%20Present%20a%20Model/Projectexample.htm
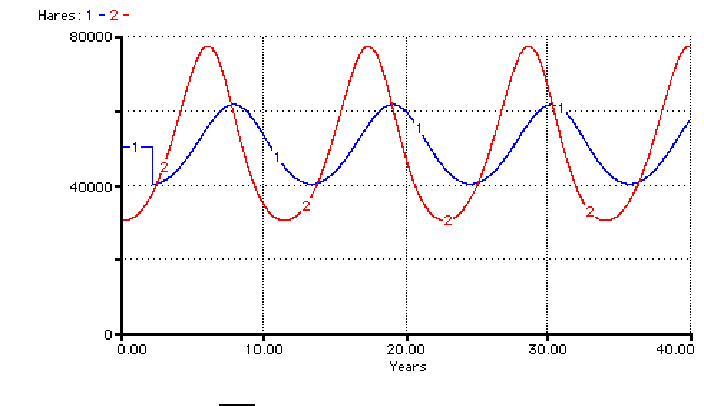
Notice that the lynx population has a slight phase delay after the hare population.
3.2 Decaying
Let the population density be n[t]. At anytime,
carriers are generated spontaneously at a rate G per unit volume
per unit time. The popuplation decays (dying) at the rate of n τ
where τ is called lifetime. Then, the population
equation is:
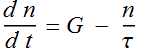
What is the steady state population?
At steady state: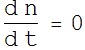 
Hence: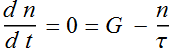 
Thus: n=G
τ
The carrier lifetime is intrinsic GaAs at room temperature is ~ 1
ns. What is the rate of spontaneous electron-hole generation?
At t=0, let population be 
,
let the carrier generation rate be P (stand for pump), what is the
population as a function of time?
We can solve the differential equation:
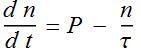
The solution is:
At
t=0: 
Hence: 
Notice that as t-> ∞, the steady state population is again: n(∞)=P τ
3.3 Diffusion
Concept of diffusion discussed in class.
see this as a demo:
http://www.youtube.com/watch?v=H7QsDs8ZRMI
http://demonstrations.wolfram.com/RandomWalkAndDiffusionOfManyIndependentParticlesAnAgentBased/
Key concepts in diffusion are gradient and flux.
Flux: the number of particles cross a unit area per unit time: F
Gradient: ∇n
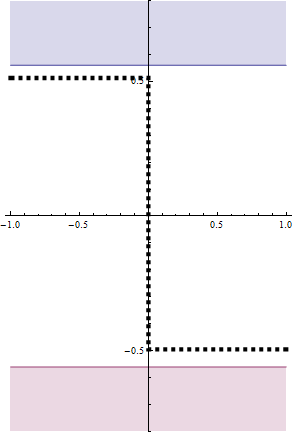
Example, what is the gradient of the population distribution
below?
To calculate the gradient:
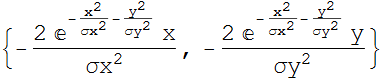
The diffusion flux is oppositely proportional to
the gradient:
F=-D
∇n
where D is the diffusion coefficient.
Since carriers are charged, as they diffuse, they generate
diffusion current:
J= e F
which is proportional to the carrier gradient:
J=- e D
∇n
Think of water streams flowing down from a hill:
Let n be the population within a volume V enclosed
in a surface. Suppose the carrier can be generated, decay, and
diffuse:
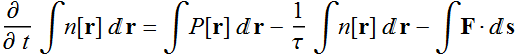
From
equation: F=-D
∇n
Thus:
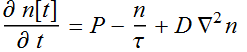
We will be using this equation in diode problem. (Example of 1D
solution is shown in next section)
3.4 Drift
Because the carriers are charged, they also respond under an electric field, giving drift current as we learn before.
4. Drift and diffusion currents
To combine both drift and diffusion current:
See homework on drift current of a photoconductor.
See homework on diffusion current in a BJT
"Diffusion" of a light pulse demonstration.
Below is a light pulse transmitted in a fiber. Notice what happens as the pulse travels.
Below is the demonstration of 2 light pulses of different initial duration
Below are two light pulses transmitted in a fiber. Notice what happens as the pulses travel.
5. p-n junction
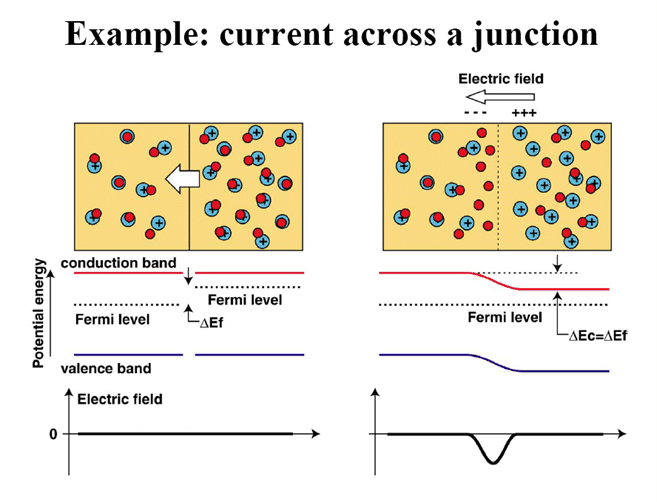
5.1 Review homework 3
Principle of detailed balancing. If we have the following case:
The left hand side Fermi level is different from
the right. What'll happen?
Carriers diffuse, left goes right and vice versa.
The rate of left going to right = density of occupied states of
left x density of UNOCCUPIED of right:
Vice versa for the other way and both MUST be equal at equilibrium
We see that this implies: 
What it means is that the Fermi Level must be equal.
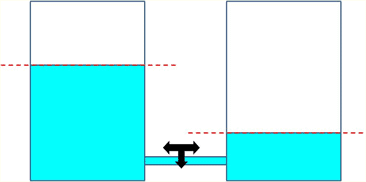
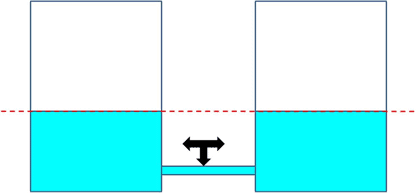
How do they get to the same level?
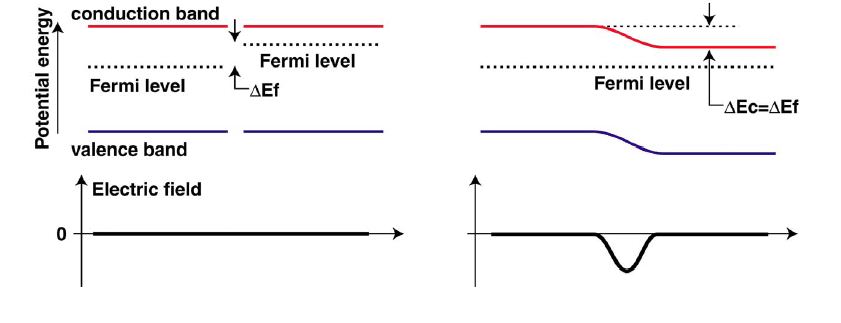
At -∞ and +∞ we have:
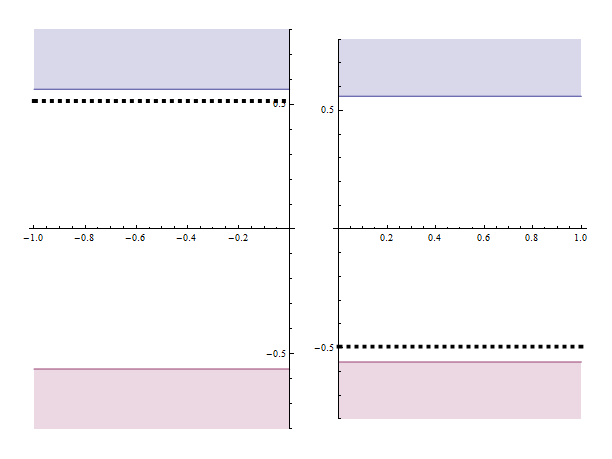
The Fermi levels at -∞ and +∞ stay the
same relative to the band. So, if they level, the band MUST shift
relative to each other. We'll learn how in Chapter 5.
5.2 Diffusion across a junction
and 
Consider just one type of carriers for simplicity.
5.3 Example of 1D diffusion
See 5.4 below for homework
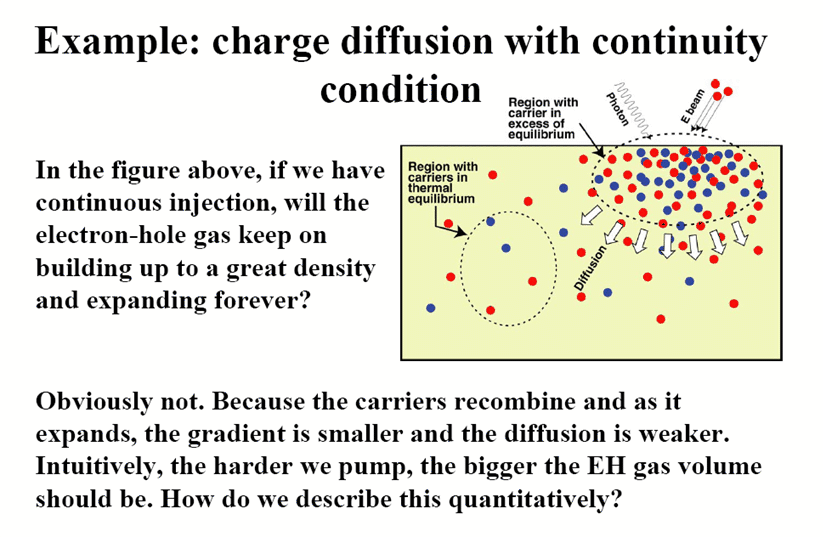
See more examples below.
5.4 For Homework
In the follow, calculate and plot the carrier density in a thin layer of semiconductor under uniform carrier pumping (either optically or by e-beam).
5.4.1 Example 1
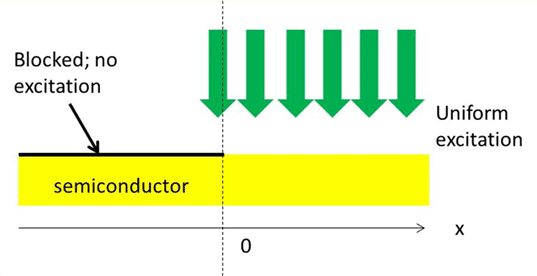
Consider the semiconductor as infinite. Let the
semiconductor be excited for just the right half. Assume that the
semiconductor layer is very thin and the carrier generation is
uniform in horizontally and vertically. Assume also that the
carrier is intrisic and its intrinsic carrier density is very low,
and we can neglect it. (In this problem, we are interested only in
excess carriers that are generated by external excitation).
Assume for simplicity that electrons and holes have the same
diffusion coefficient and they diffuse together (ambipolar
diffusion). What is the carrier distribution and its flux at
steady state?
We start by solving the steady state diffusion
equation. Let n[x] be the carrier density:
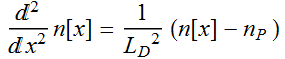
where 
, P is pump rate or the number of carriers generated per second,
per unit volune, and τ is the carrier lifetime. Recall the
definition of diffusion length above: 
where D is the diffusion coefficient.
Hence, the most general solution is: 
.
Applying the solution of each half of the semiconductor. For the
left half, we can’t have non-vanishing term 
because it would mean carrier density approaches to ∞ at x->
-∞. Also, the pump rate is zero for the left half. Hence, the
solution is:
where we use the term 
instead of 
to indicate that 
is the carrier density at x=0.
The flux
is: 
The thing we don’t know is 
.
For the right half, it is:
in which we drop 
for the same reason at x-> ∞.
We can rewrite it slightly differently by defining
a quantity 
such that:
Then: 
The flux
is: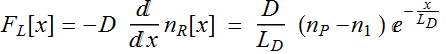 
The thing we
don’t know is 
.
We can plot the solution below:
How do we determine 
and 
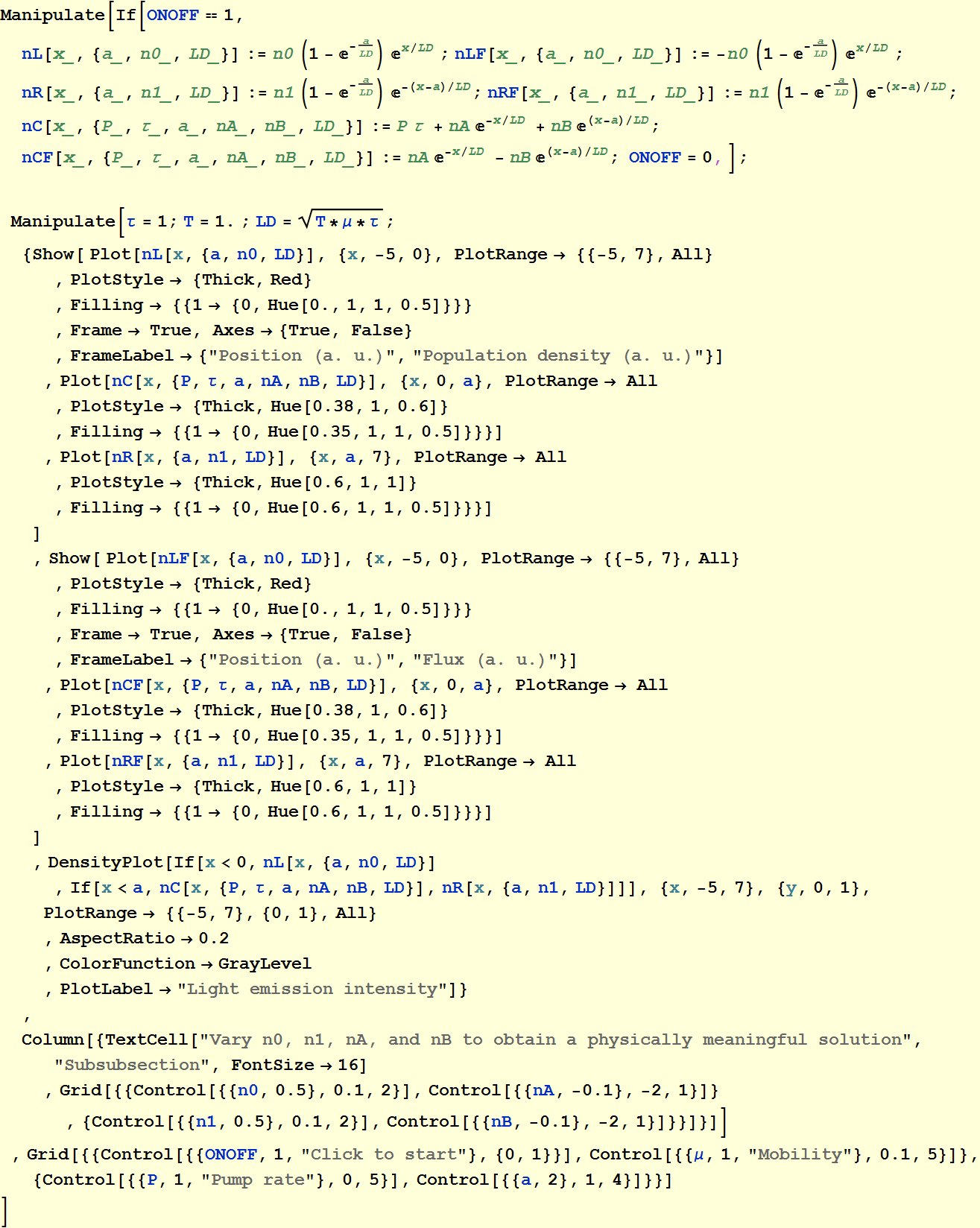
5.4.2 Case 2
See explanation in section 5.4.1 above. In this case, only one segment of the semiconductor is excited. We now have 3 segments: left, center, and right. The solutions are
where we introduce the factor 
just for convenience. It is just a constant, but we’ll see that it
is quite convenient for the determination of 
and 
.
For the center, we have the most general
solution:
.
here, we can keep both 
and 
because neither term gives us ∞ like the left and right solution.
We can rewite it:
.
So, here, we have
4 unknowns: 
,
and 
(Guess what simple relationships there might be between 
,
and 
,
)
We can plot the solution below:
6. Ambipolar (bipolar) carrier diffusion
When the diffusion involves opposite charge
carriers, we call ambipolar diffusion. It is relevant only when
both populations are significant relatively (not when one is much
>> than the other). Examples are in p-n junction with
comparable doping, optical pumping. The main effect is that they
diffuse together because of electric force attraction that will
pull one population back to the other if one diffuse faster than
the other. Electrons generally diffuse faster than holes in most
semiconductors (
).
But it doesn't mean electrons will diffuse away from holes. They
will maintain charge neutrality.
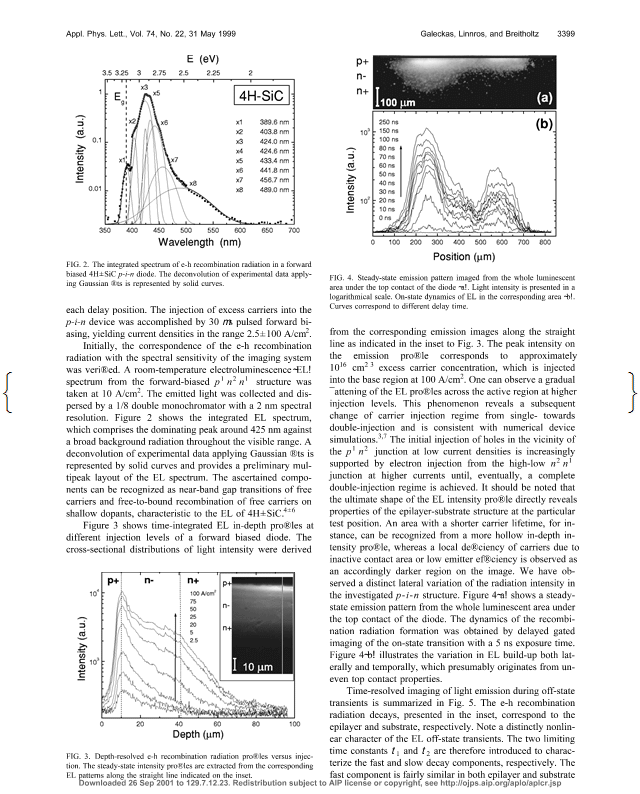
7. Example: a professional research paper
