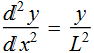in the form of Sinh or Cosh Homework 4 - part B
ECE 4339
Han Q. Le
(copyrighted) U. of Houston
1. Diffusion differential equation
1.1 Solve the differential equation
by obtaining the most general
solution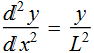
in the form of Sinh or Cosh
Answer given
Since we know that: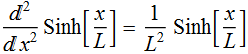 
and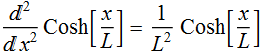 
the most general solution can be written as a linear combination:
where c1 and c2 are constants.
1.2 Dirichlet boundary condition
Let y[a]=A and y[b]=B, obtain 2 equations for unknown coefficients. Then, solve for them and substitute to obtain the complete expression for y[x].
1.3 Simplified expression
Do you think this is an expression the
solution?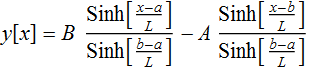 
.
Prove it.
1.4 Can you show your result in 1.2 agrees with that in 1.3? (skip if you don’t like algebra)
1.5 Numerical illustration
Let L=1, a=0, b=3., 
;
,
plot the solution on linear scale and log scale from a to b.
Then do it again for 
;
B=1.,
App: carrier concentration in base
1.6 Diffusion current
If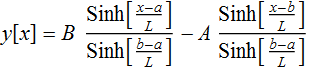 
represents
carrier density, what is the diffusion current?
(The answer is: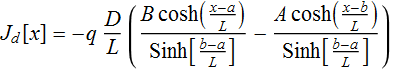 
)
1.7 Numerical illustration of diffusion current
Let L=1, a=0, b=3., 
;
B=1., D=1 and charge q=1, plot the
diffusion current solution on linear scale and log scale from a to
b.
App: Diffusion current in base
2. Optically pumped semiconductor: pumping on one half side.
2.0 Review
See Lecture Chap 4, part 2, section 5.4.1
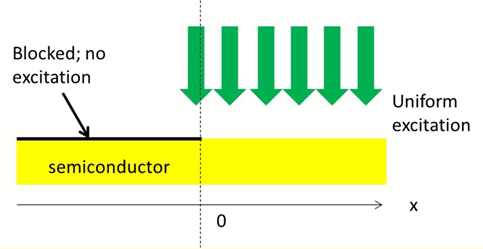
Consider the semiconductor as infinite. Let the
semiconductor be excited for just the right half. Assume that the
semiconductor layer is very thin and the carrier generation is
uniform in horizontally and vertically. Assume also that the
carrier is intrisic and its intrinsic carrier density is very low,
and we can neglect it. (In this problem, we are interested only in
excess carriers that are
generated by external excitation).
Assume for simplicity that electrons and holes have the same
diffusion coefficient and they diffuse together (ambipolar
diffusion). What is the carrier distribution and its flux at
steady state?
We start by solving the steady state diffusion
equation. Let n[x] be the carrier density:
(2.0.1)
where 
, P is pump rate or the number of carriers generated per second,
per unit volune, and τ is the carrier lifetime. Recall the
definition of diffusion length above: 
where D is the diffusion coefficient.
2.1 Obtain a most general solution of Eq. (2.1) above
Answer (given, but you are welcome to obtain your own answer)
2.2 Apply solution of 2.1 just for the dark half (left half)
In the dark half, there is no pumping, which means nP=0, what is the most general solution that does NOT violate any physical limit (it should NOT go to infinite at any point or at infinity). Rename your coefficient(s) with subscript L to indicate that they are only for the left half and apply subscript L to carrier density to indicate that it is the solution for left half.
Answer (given, but you are welcome to obtain your own answer)
2.3 What is the value of carrier density at x= -∞?
2.4 Obtain a solution for carrier density in the left half.
Let the boundary between the dark and light region
be x=0. Denote 
be the carrier density at 
on the dark half, obtain a solution for carrier density.
2.5 What is the carrier flux 
in the dark half (left half) from the result in 2.3?
Hint
Take derivative of
(2.4.1) 
2.6 Apply solution of 2.1 for the optically pumped half (right half)
Here, nP ≠ 0. Determine a solution that does NOT violate any physical limit (it should NOT go to infinite at any point or at infinity). Then, use subscript R (right) for all symbols to distinguish from those of left half.
Hint
For the right half, the general solution from Eq.
(2.1.1) is:
(2.6.1)
However, one must drop one of the 2: either 
or 
(which one and why?)
2.7 What is the value of carrier density at x= +∞?
2.8 Let the carrier density at 
be 
,
obtain the solution of carrier density in the right half.
Hint
The correct answer
is
(2.8.1)
2.9 Calculate the carrier flux for the left half based on the solution above.
2.10 Graphical solution
Based on the results obtained from 2.4, 2.8, we can
plot the carrier density solution for each half if given 
,
and nP. We can also plot the fluxes. The APP below lets us choose
ratios 
and 
to see the carrier density on each half. However, can we
arbitrarily choose any values for 
and 
?
In other words, does nature pick specific solution with unique
values of 
and 
or does nature leave it to us to pick 
and 
to our heart delight?
Run the APP, select values of 
and 
that you think give correct solution, copy and paste in and
explains why.
APP: Carrier distribution in optically pumped semiconductor
2.11 Obtain 2 graphical results for the lowest and highest mobility. Compare and discuss about density and flux
3. Analysis of paper on p-n diode electroluminescence
Read the paper: “Time-resolved imaging of radiative recombination in 4H-SiC p-i-n diode” by A. Galeckas et al., Appl. Phys. Lett. Vol. 74, pp. 3398-3400, 1999. It is available on the last section of lecture Chapter 4, part 2.
To answer the questions below, you need to read the paper. Looking at a figure alone will NOT be enough. Read those paragraphs pertaining to each figure to answer them. You do NOT need to understand 100% of what in the paper to answer all these questions below.
3.1
Label on Fig. 1 (copy and use some software such as ppt drawing to show) where the substrate is, the epilayers and their thickness, the mesa and its dimension.
3.2
What does figure 2 describe? What color do you think it looks like?
3.3
Look at Fig. 3. Look at the black-white inset photo. What is the bright streak at the top? Why does it get darker as you go to the bottom?
3.4
Look at Fig. 3 again. What does it plot? Is the
vertical axis on log scale or linear scale? If we assume that the
emitting light intensity is proportional to the electron-hole (EH)
density, how do you express the spatial variation of the EH
density along these layers? Look at the curve for 100 A/cm2, if
you approximate the carrier density profile as 
where x is the distance and 
is the diffusion length, what are the diffusion length values for
n- and n+ region?
Help to answer this question:
(see HW 4A, APP How to find an exponential coefficient in problem 3)
APP: How to find an exponential coefficient - applied to diffusion length
3.5
Recalling that diffusion length 
where D is the diffusivity and τ is the effective carrier
lifetime, let’s assume that the D is the diffusivity is
approximately the same for both n- and n+ region, which region, n-
or n+, has a longer carrier lifetime? Can you speculate why so?
3.6
Recalling that the diffusivity D is also proportional to the mobility. Which region, n- or n+ do you think the mobility is higher? Do you think that both mobility and carrier lifetime contribute to the difference in the diffusion length between the two regions?
3.7
Look at Fig. 4. What does the top photo (Fig. 4(a)) show? Copy and paste the figure and draw a arrow to show where you think there is an excess electron-hole population. Do you think that this is a spatially uniform diode along the horizontal direction? In Fig. 4(a), which part, left or right, is more efficient as an LED? What does Fig. 4(b) show? Is the vertical scale logarithmic or linear?
3.8
Look at Fig. 5. What do the researchers claim the effective carrier lifetime they measured for each region, n- and n+? How did they measure these values?
3.9
Go back to questions (3.4) and (3.5), use the lifetime given in the paper you that you find in question (3.8) above, use the value of diffusion length you find in (3.4), infer what you think the diffusivity for each region are, using appropriate relations.
3.10
Comment on what you learn from this paper
