There are many such materials, quartz is a very commonly used one.
Q & A about retarder
Some students had question about retarder waveplate and were confused about the convention. Below is the answer.
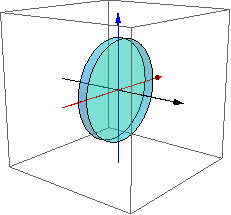
A retarder
Below is an image of a common birefringent crystal:
calcite (a calcium carbonate crystal or feldspar).
There are many such materials, quartz is a very commonly used one.
Consider a thin waveplate on the right. It is birefringent: the E field parallel to x axis (red, horizontal) has an index of refraction that is different from that along y axis (blue, vertical).
Let the x-axis index be 
and y-axis be 
,
and l be the thickness.
An E-field that has BOTH x and y component will have a phase
difference between them after going through the plate:
; 
And:
In unit of cycle instead of radian, it is:
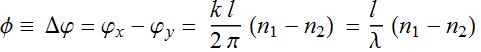
Usually, 
is a certain specific fraction of λ (modulo λ), such as 1/4 or 1/2
and we call it quarter-wave plate or half-wave plate.
If 
is,
for example 6.25 λ, it is the same as 0.25 λ (modulo λ0 and we
call it a quarter-wave plate although strictly speaking, it is a
lot more than a quarter.
Likewise, if 
is,
for example 9.5 λ, we still call it half-wave plate.
Convention about retarding and phase sign
In the above, the axis with smaller index called
fast axis, the
other is called slow
axis for obvious reason. If x is the fast axis, and y is the slow
axis, then:
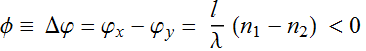
This is consistent with our convention of using algebraic notation
for phase retardation: instead of saying retard or advanced, we
just use the sign: negative means retard or late (for the slow
axis component), and positive means advanced or early.
Think of this analogy: an airplane is scheduled to arrive at 8:00
AM, but is late and arrives 8:20 AM. Then the time discrepancy:
8:00 AM- 8:20 AM = -20 minutes is the loss time and negative. The
opposite is extra time gain and positive. If it arrives early, say
20 minutes, you have an extra 20 minutes time to spare, as
opposite to -20 minutes loss from your schedule if late.
That way we don’t have to say the phase difference is retard or
advanced, but just base the calculation on the sign. However, a danger: watchout for the effective
sign after you modulo a quantity by λ. See example below.
Demo
In the above, it is like this: Suppose you are due to arrive 8 AM Monday, but the plane is so late that it arrives 5 AM Tuesday, which means 21 hrs late. However, if someone who lives in “Ground Hog Day” doesn’t know you are supposed to arrive Monday and knows only that you are supposed to arrive 8 AM, it appears you are 3 hrs early.
Answer to homework
The phase difference between the fast and slow axis
in terms of cycle (2 π radian) is:
Its value is:
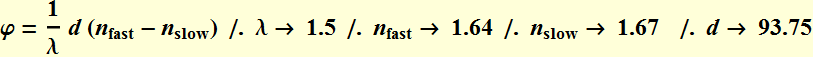
The wave plate phase shift value is -1.875 or
effectively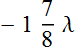 
.
But the phase shift must be modulo with respect to λ, which means
add or subtract an integral multiple of whole λ to bring it to
within +λ/2 or -λ/2.
We must modulo this quantity with 2 λ to bring it into [-λ/2, λ/2]
interval, which means that is it
-1.875
+2= 0.125 λ
Note that each λ-> 2
π.
In terms of π, it i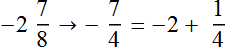s 
. Hence, it is a case of being so late (like 1 day and 18 hrs)
that it appears early by π/4 (6 hours).
