Important note:

Lab. II is to explore Kirchhoff Voltage law and Kirchhoff Current law. There are two versions of the lab:

•   Basic version: linear circuit with resistors. The basic version in MS format can be downloaded from the course web page. Apps for help are on this page.

• Advanced version: non-linear circuit with resistors and LEDs. Since LED is non-linear, the problem can only be solved with numerical approach for either Node-Voltage or Mesh-Current method.

2. TThis page is the advanced version. It is designed for those students who wish to explore and learn about LEDs. The score for the advanced lab work is higher, 150 pts instead of 100 pts to reflect the higher complexity of the circuits.

Prior to the start of Lab. II, you must make a commitment to either the basic or advanced version by submitting the pre-lab prior to starting. Once you commit to a version, you must follow through with lab work. In other words, your pre-lab and your lab work must match.


Introduction:

There are three circuits to be built in succession by simply adding to or swapping elements of a previous circuit to obtain the next. For each, perform measurements as specified.

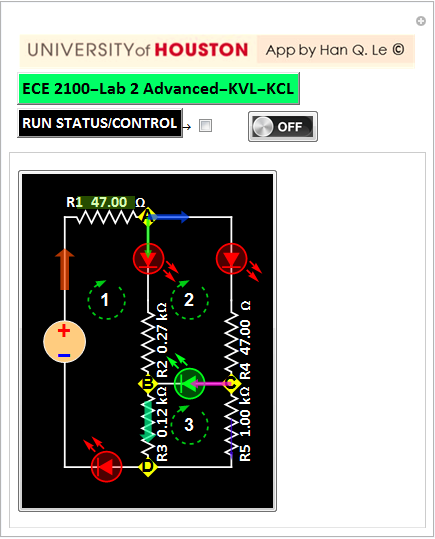
Circuit 1	Circuit 2A	Circuit 2B

Since the circuit cannot be solved with linear (matrix equations) method, we must use numerical approach.
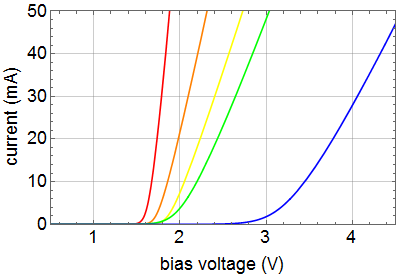
First, let's take a look at LED circuit behavior:

Current vs. Forward Bias Voltage for red, orange, yellow, green, and blue LED	Forward Bias Voltage vs. Current

A typical LED is different from a typical diode with regard to two properties:
1- the contact potential is substantially higher and is a function of the bandgap of the material, which determines its color;  and
2- its conduction above the contact potential is more resistive than diode.

Hence, the ideal diode model is neither relevant nor useful. As we can see above, different color LEDs have different I-V characteristics that must be realistically taken into calculation. Furthermore, the above curves are only nominal, as there is great variation of electrical characteristics among nominally the same color LED's, and the variation can be significant even among those from the same batch by the same manufacturer. The reason is that the series resistance and the thermal behavior are quite sensitive to the fabrication process and packaging. Hence, the above phenomenological model is useful as a rough guideline, but a circuit can only be calculated accurately only with actual specific device data.

Numerical methods for KVL equations

For the three above circuits, The three sets of KVL equations are:

If you are curious how the above equations can be coded to do numerical calculation, here is the code for Circuit 2A (you can do minor modification yourself for other circuits). Here is the Mathematica notebook that you can download and run. (Just select, shift+enter)

The first circuit is quite simple with just two equations as shown at the top set. The other two circuits, 2A and 2B involve a bi-directional LED, which has different characteristics for the two directions. One is a green LED, the other is amber. Circuits 2A and 2B involve swapping the positions of resistor R2 and R3, and the positions of R4 and R5. This results in opposite current direction through LED4, which is the bi-directional and the color change serves as a current indicator.

The above sets of equations are numerically solved using multivariate secant method in the app explained below.

The circuit can also be solved with KCL equations, i. e. the Node Voltage Method. However, numerically, this method is less advantageous compared to MCM as we can see below.
The unknown variables to be solved for are high-lighted in green.

Clearly, there are more equations to solve, and a practical algorithm is as follow:
1- Assume initial value of vled1, vled3, vD.
2- Solve for vA, vB, vC
3- Substitute vA, vB, vC and solve for vled1, vled3, vD.

Iterate until satisfactory results are obtained. It is more labor intensive than the MCM that have fewer variables.

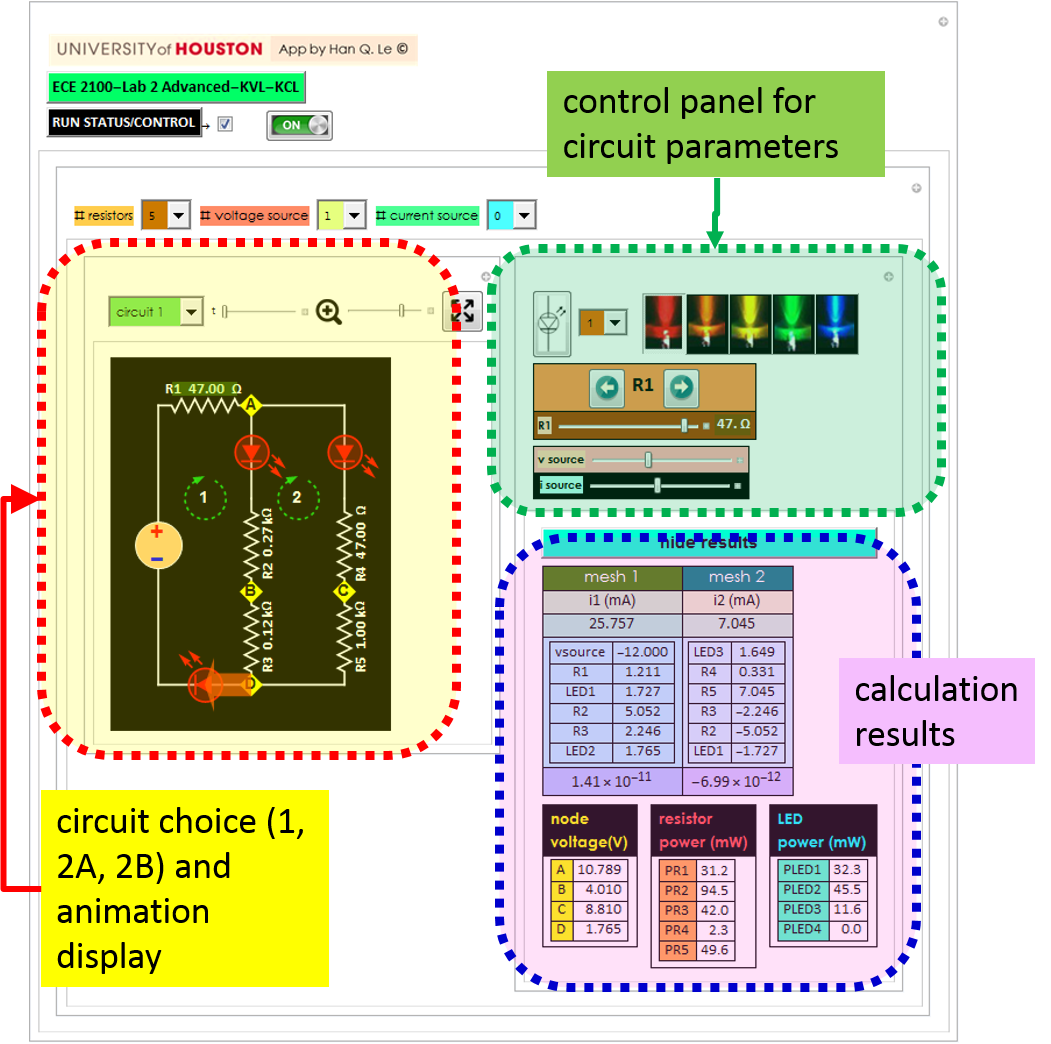
Main app for the Lab

	The app has 2 panels: The left panel provides choice of the circuit, animation control and size of current arrow. The right panel provides controls for circuit parameters and optional display of calculation results.
For .cdf file: For slower computer, a slightly less graphical app is here

The circuit is designed for the default resistor values to illustrate the effect. The values should not deviate more than +-25%. The LEDs can be any of the five most common colors. They do not have to be the same for all three, each can have its own color. Only LED 4 is special. However, one can, in destitute, substitute the bi-directional LED with two parallel and directional-opposite LEDs.

It is important to keep in mind that this calculation is based on the phenomenological model of LED characteristics shown above. Actual LEDs can be different, hence exact agreement between calculation and experimental results should not be expected. However, that is not important. The objective of this lab is to demonstrate KVL and KCL. Hence, you are expected to do measurements of voltages of the various meshes and add them up to verify that they are zero within experimental uncertainty.  You will also measure the node currents at two nodes: B and C to verify KCL.

Lab work outline - please see write-up for details

For pre-lab, also follow the red letter  in the write-up.

Step 1 - Circuit 1

1.1  You will be given 2 x 47 Ohm or 50 Ohm resistors.  Although you should have the resistors or LEDs listed, you can choose similar elements based on what you have. For example, if you have yellow LEDs instead of red, you can certainly use them, or mix whatever colors you have. For resistors, you can use a substitute that is within ~±25% of a suggested value if you don’t have the right one.
Once you start, stay with the same elements you have, in other words, don’t change resistors or LEDs from one circuit to the next. All three circuits are really of the same basic configuration

1.2

1.3

 1.4  Perform measurements and record the results based on Table 2 above.  In your Lab notebook, you must tabulate and clearly show a column for calculated values of voltages and currents (based on the APP with actual values of your resistors) and a column of corresponding measured values. Next to these two columns is the relative deviation. Your deviation can be easily 5, 10% or more, because LEDs have great variation, even by the same manufacturer within the same batch. But that is not important. Your actual measurements are what important here.

1.5  Test Kirchhoff voltage law. Add the measured voltages of all the circuit elements in each loop. KVL states that it should be zero. Take your results, divide it by the root-sum-square of them, that is your figure-of-merit, report and write your discussion (e. g. KVL is verified up to 1 part in 10^4, limited by instrument precision, etc.)

                                                                               

Step 2 - Circuit 2A

2.1

2.2

2.3   Create Circuit 2A by inserting the given bi-directional LED between B and C such that you get green light instead of amber. Perform the same type of measurements and test as you did in 1.4 and 1.5 above. Tabulate your results neatly.

2.4   Report what you observe about the relative brightness between LED1 and LED3 before and after inserting the special LED (LED4).

2.5  Test KCL law: Perform current measurements at node B and record in your lab notebook like Table 4 below (make sure you get correct sign. Negative for the first 2 and positive for the last).

                                                                                                                                                  

 Step 3 - Circuit 2B

3.1

3.2

3.3

3.4  Build Circuit 2B by doing what you observe in 3.1. Report in your lab notebook color change of LED4 and discuss what causes it. Do you think what applications bi-directional LED can be used for?

3.5   Perform the same type of measurements and test as you did in 1.4, 1.5, and 2.3 above. Tabulate your results neatly in your lab note book. Comment on your KVL test.

3.6   Test KCL law: Perform current measurements at node C, do what you did like 2.5 above. Again, discuss how good your KCL test is at this node.

 

 Step 4 - Discussion and Conclusion

Write what you think of your study of KVL and KCL of this lab. Do you think LED is a good indicator of current flow? What do you learn (personally) in this lab?