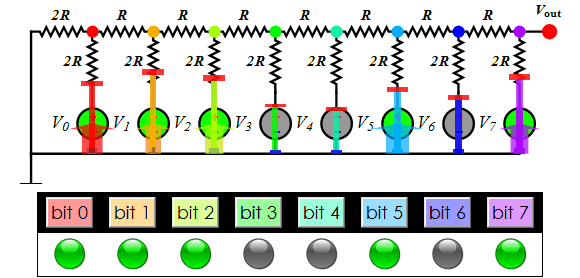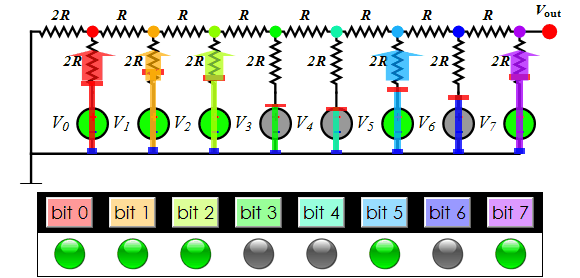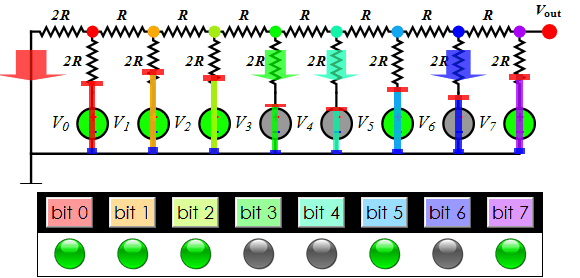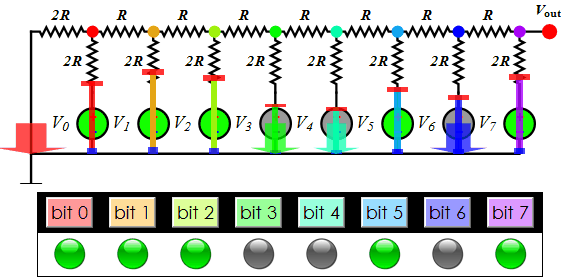
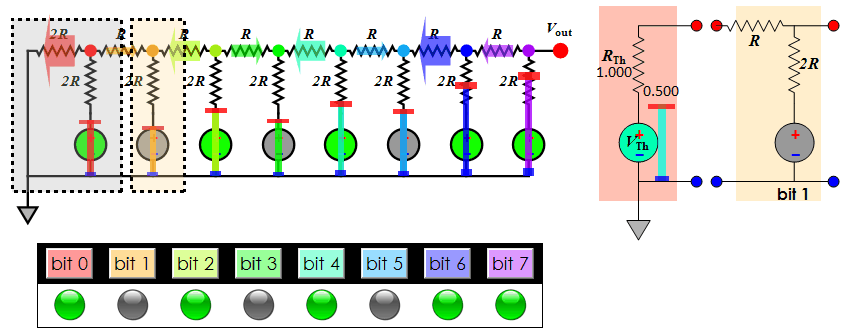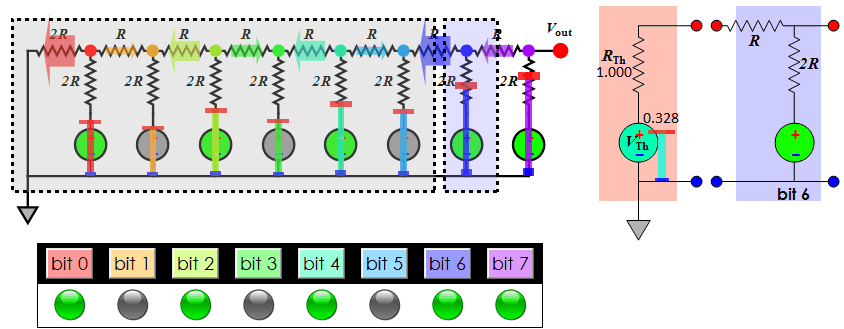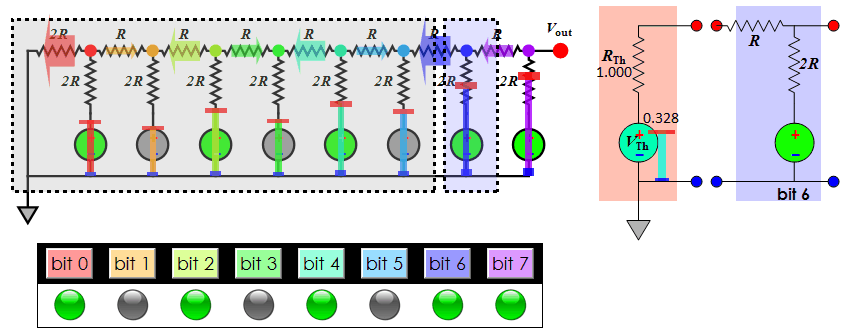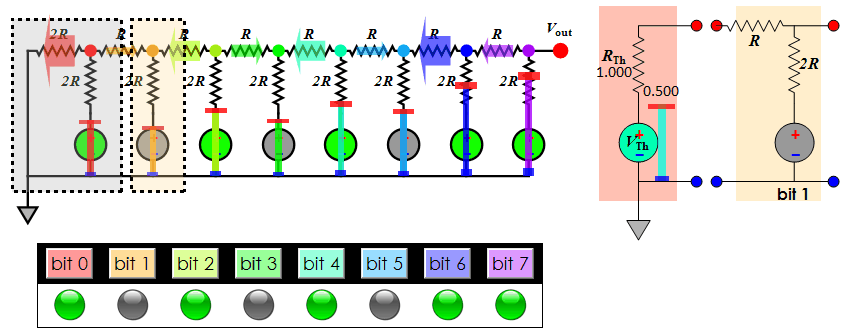
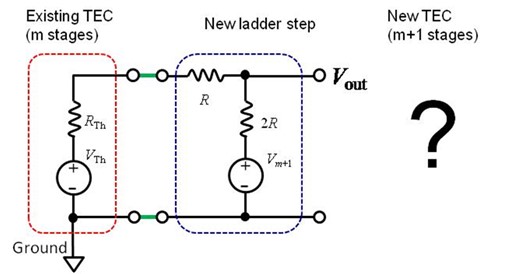
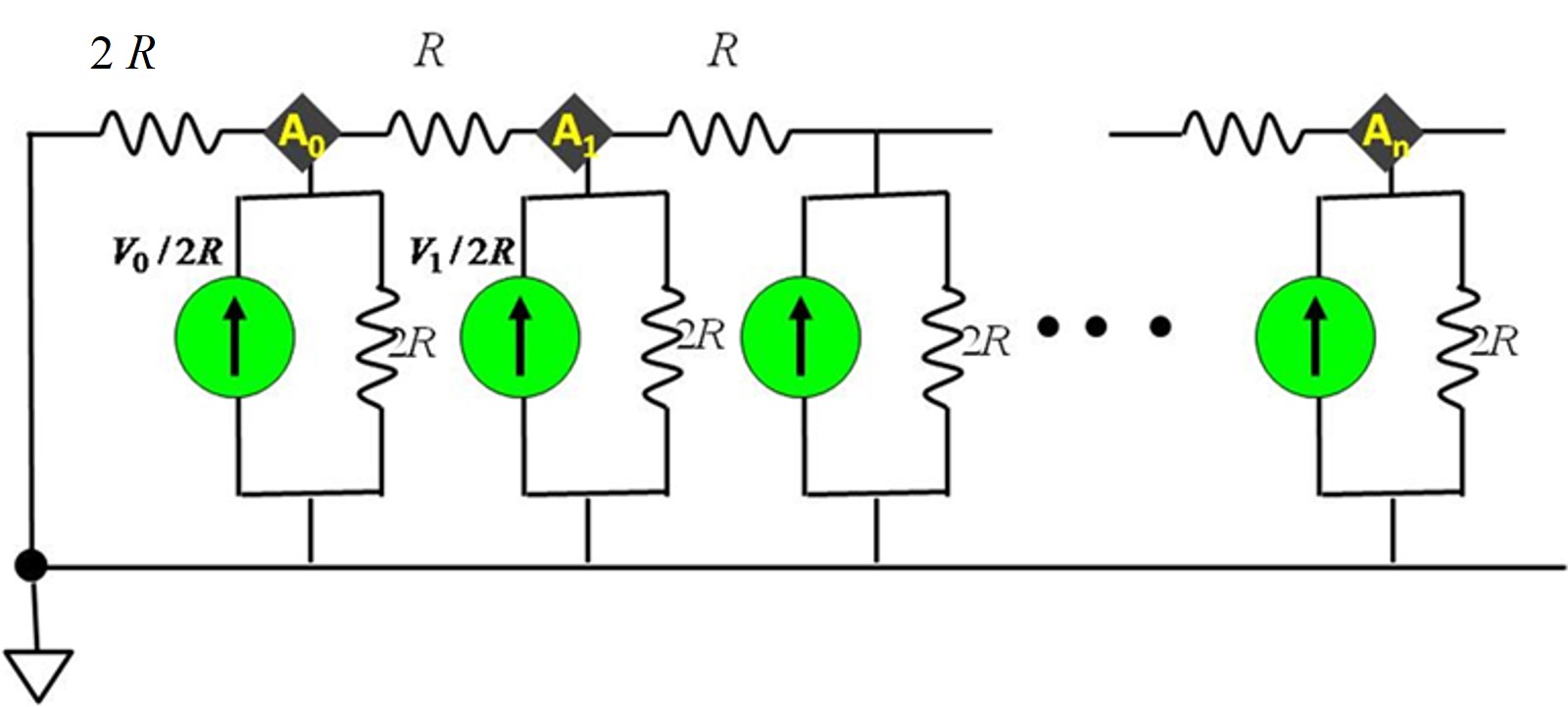
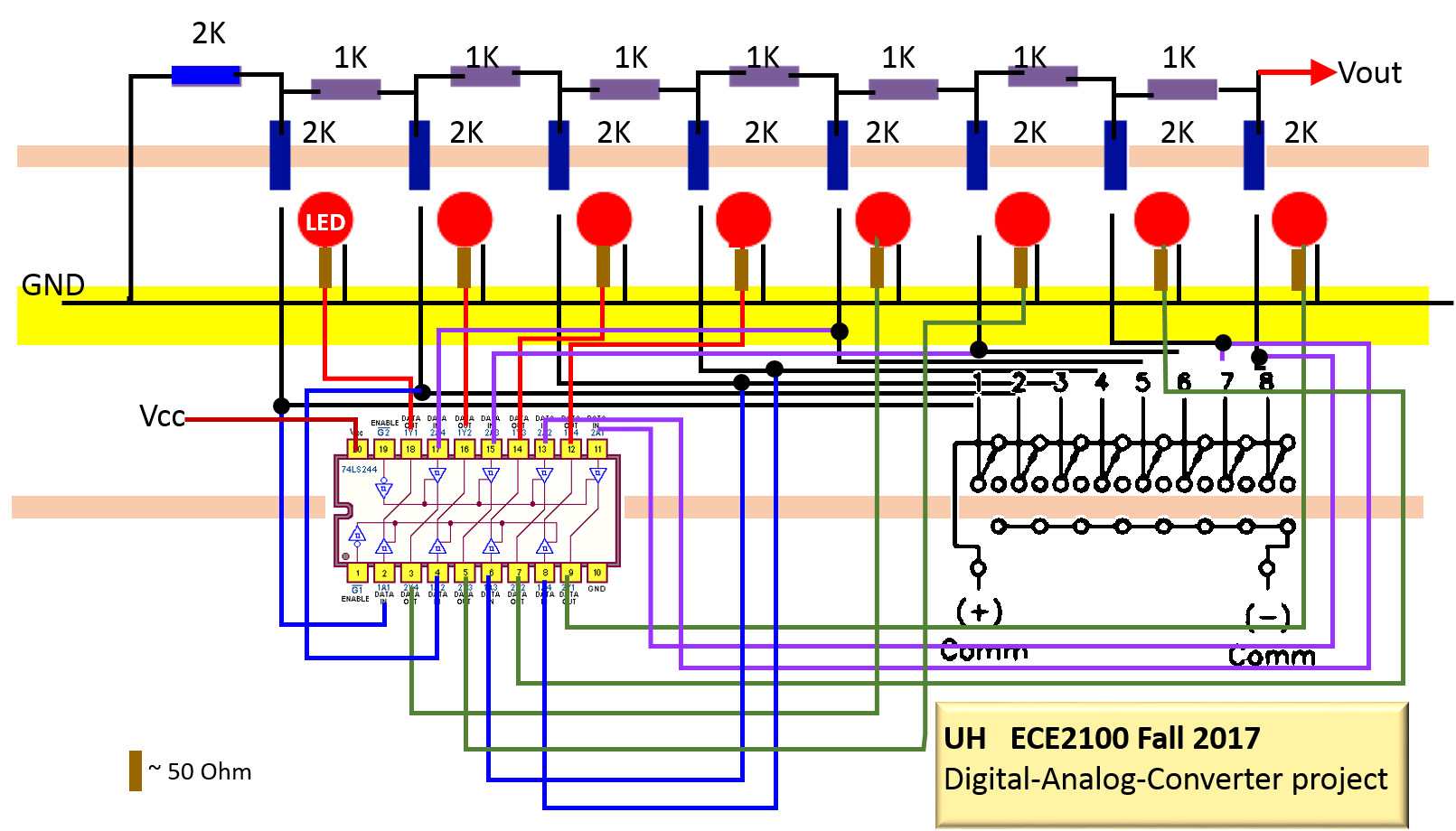
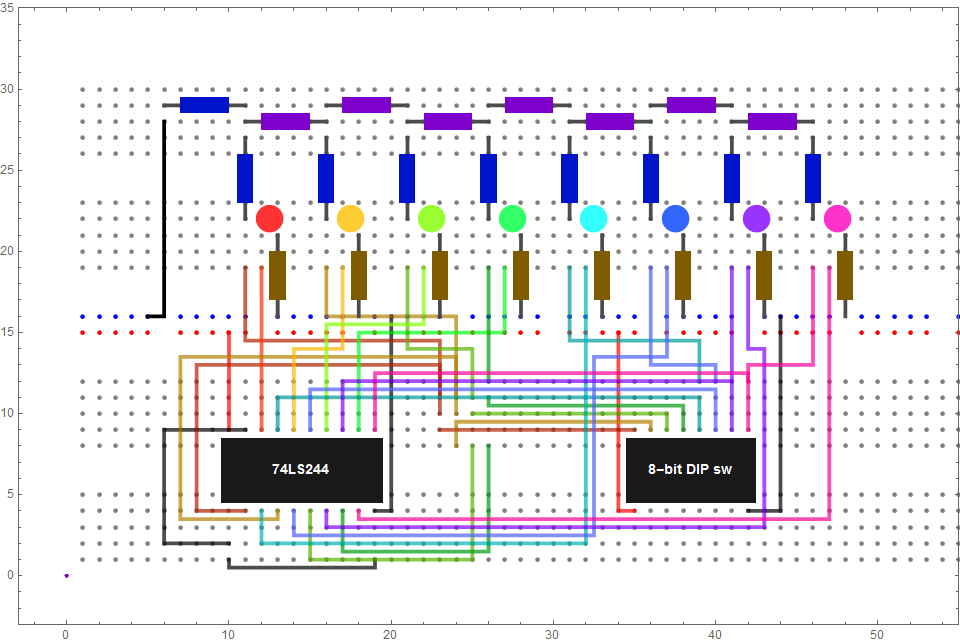
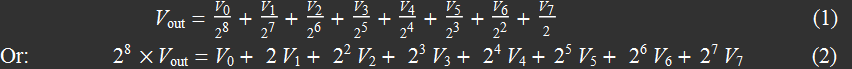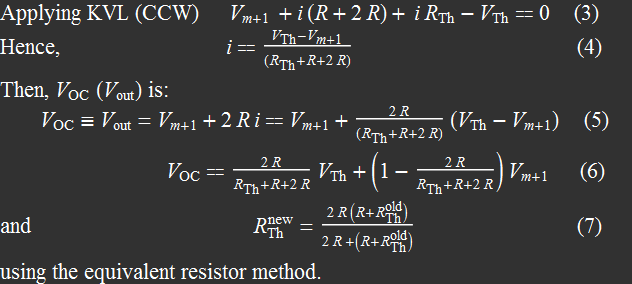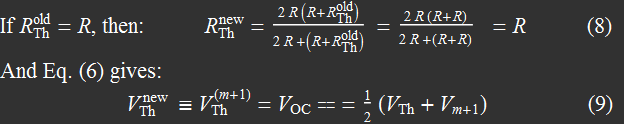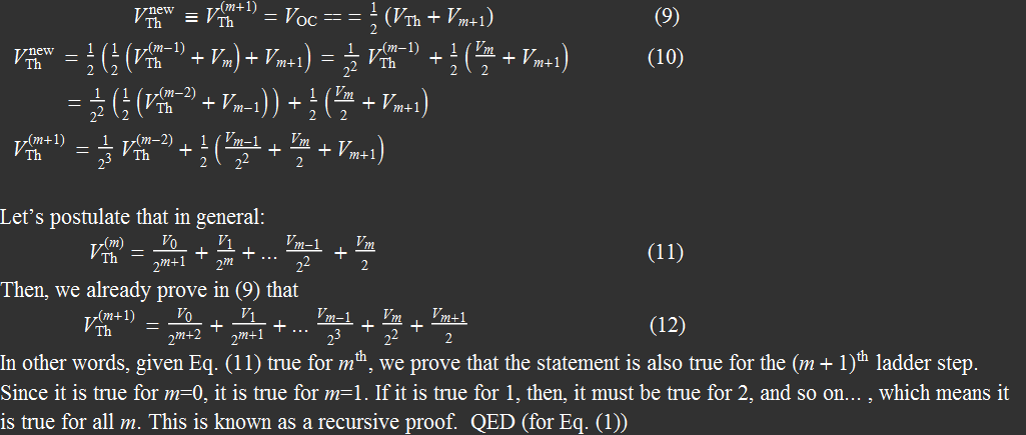About
running apps:
- If you
have Mathematica(R),
download the .nb
APP files.

- If you
don't have Mathematica(R),
you will need to
download the
free Wolfram
CDF player
. Then download
.cdf
 APP
files and run.
APP
files and run.