‎

Apps page 1

Apps page 2

Apps page 3

Apps page 4

Apps page 5

Apps page 6
Lab V-A - Active RC circuits:  Capacitors and RC Circuits

Please go to this page for full write up of Lab V-A. Below are only apps for the Lab.




Lab V-B (old) - Passive RC circuits and Measuring time constant


Topics to explore: connecting the oscilloscope probe across the capacitor to observe signal integration, and connect across the resistor to observe differentiation.
The 1st app below simulates the signal response for each case. The second app illustrates the concept of Fourier analysis and synthesis. You can synthesize different input signals such as square, sawtooth ramp, etc. with Fourier components. Notice how the signals asymptotically approach the ideal designs with higher and higher number of Fourier components. Through an RC filter, each Fourier component has a different response function, leading to the output signals as shown.

For lab measurements, you are supposed to use various R and C to observe the different time constant values. On an exponentially decay curve, you can use the 1/e (~3/8) point on the curve to get a quick estimate of the RC time. However, if you do rigorous analysis, the best way to measure the RC time is to determine the linear slope of log(signal), as illustrated in the 3rd app. Notice that you can move the cursor around quite a bit and still get a consistent RC time value, unlike the 1/e-approach that requires the precise placement of the cursor and an accurate value of the zero level. Print your regression graphics, staple or glue to your lab notebook report.
Lab V - RC circuits and Measuring time constant

Basic RC circuits (filters) with integrator and differentiator. This app is for illustration, not actual circuits you will do for Lab V (see App 4 in the right)

   
Illustration of Fourier analysis and synthesis for RC circuits.

      		Measuring RC time constant using log plot and linear regression of the slope

   
Circuit simulation for lab measurements

   

Basic RL circuits (choke)

   





A further note for students who have had, or currently take  Signal Analysis ECE 3337 or those who wish to look ahead to ECE 3337

At this point you have learned Laplace transform and its application to circuit transient response. This course is NOT supposed to teach you circuit theory, but only to provide laboratory support to your studies of circuits. However, it is useful to review and reinforce your learning whenever possible. The circuits for Lab 5 are extremely simple but they serve as useful examples of applications of Laplace transform technique. You are supposed to do some straight forward calculation of various RC time constants. But do you wonder how to simulate the signals on an oscilloscope?

You need to solve the circuits and it is a good occasion to reinforce the learning of Laplace transform.

Apply LT to circuit 2, we replace the capacitor with its Laplace transformed impedance as shown (assuming capacitor with zero charge as the initial condition).

 Both the capacitor and resistor R2 are just parallel impedance and we can replace both with their equivalent impedance as shown:
It is straight forward to apply KVL to calculate the current:

 And the output voltage is obtained as shown.

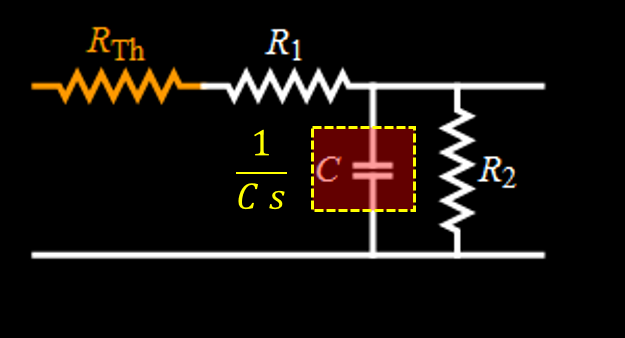
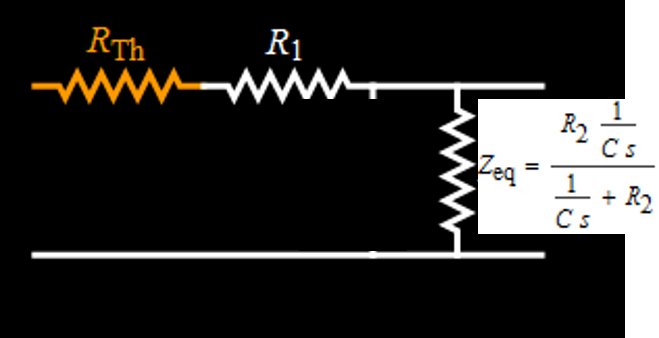
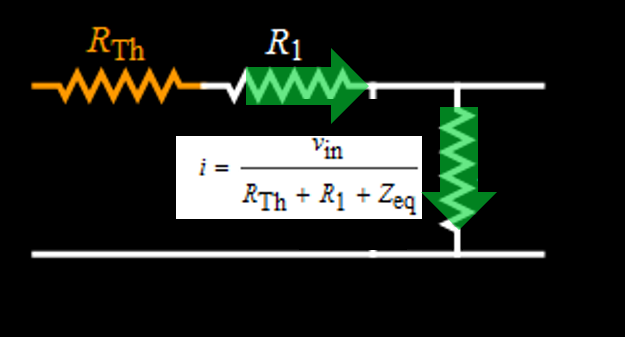
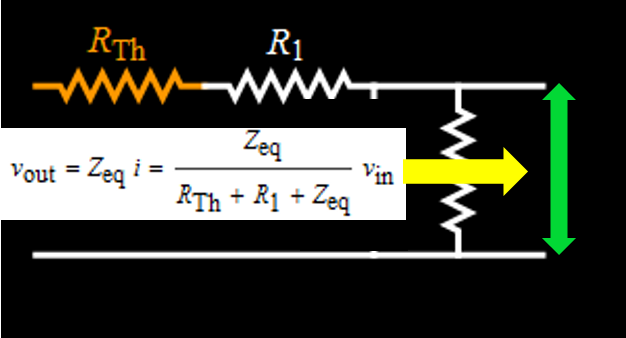
The rest is just algebra. We plug Zeq in the expression for vout (really, just tedious algebra but very simple in concept)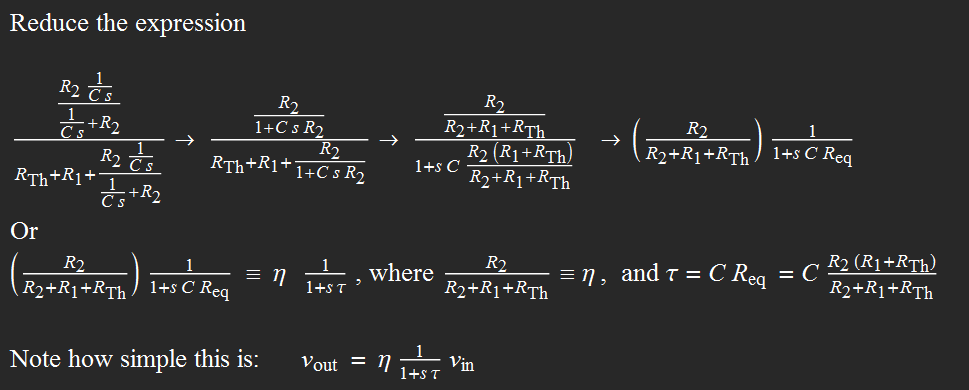



Discussion

Note something here: the "R" in the RC time constant is the EQUIVALENT resistor of the parallel circuit of (R1+Rthevenin) and R2. The serial equivalence for R1 and Rthevenin is expected, because they are in series, obviously. But why is it parallel for R2 with (R1+Rthevenin)? It is because they are indeed parallel when the voltage goes to zero. The lower the load resistance R2, the quicker the capacitor discharges. The Laplace transform method shows clearly how they are connected, resulting in an effective time constant.

Also, note the amplitude eta, which is the divider voltage of R2 for serial R1, R2, Rthevenin. This is also obvious, because for a given constant source voltage, R2 voltage is its divider portion for the three in series. Again the Laplace transform method gives the result in a simple and straightforward manner.
 
Laplace transform and inverse Laplace transform

Now we have to find the Laplace transform of vin, which is just a square pulse in this case. Then we have vout Laplace transform and all we have to do is to get the inverse Laplace transform of Vout to get its time function expression. The whole deal is captured in the figure below: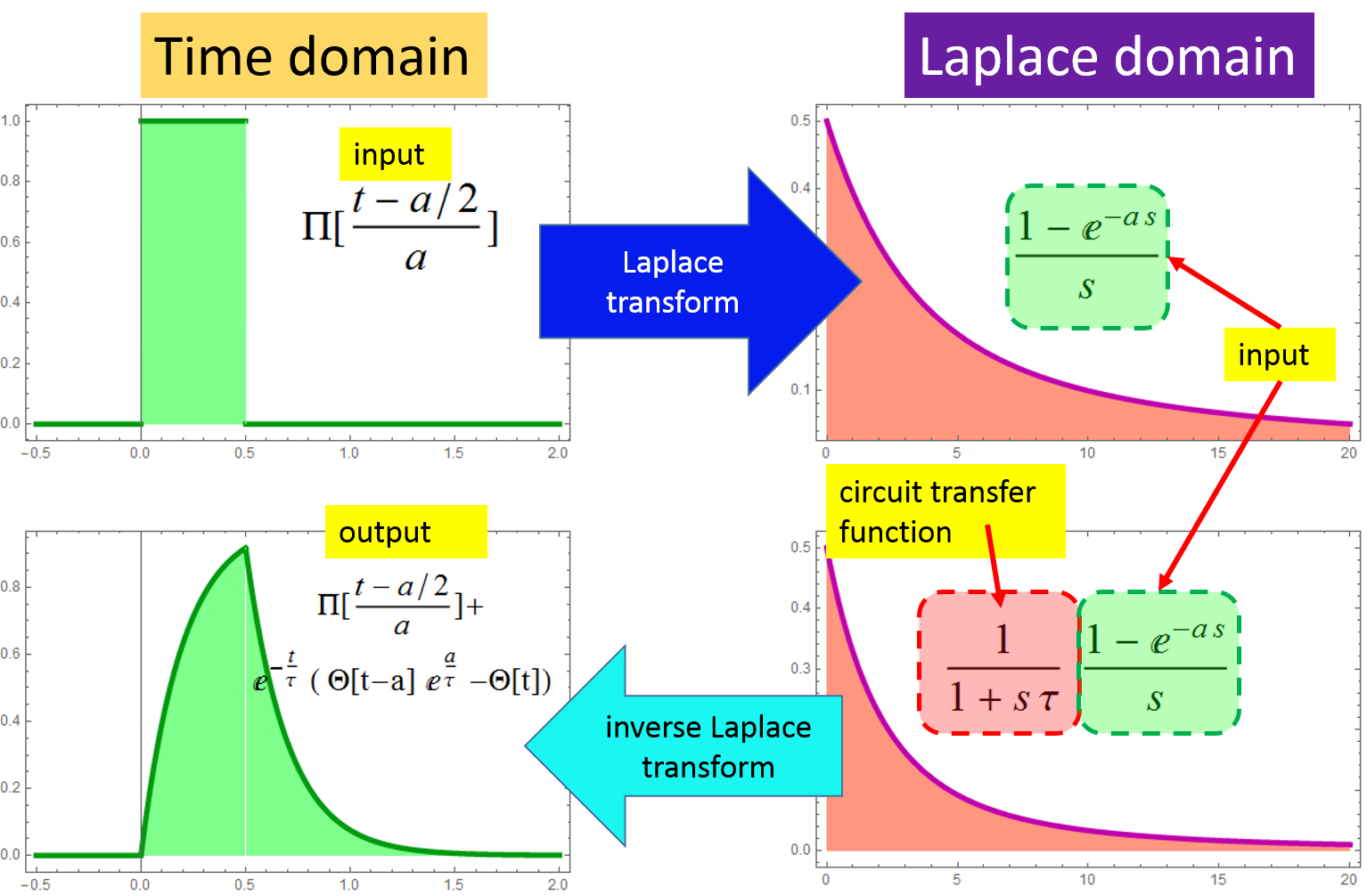



Hence: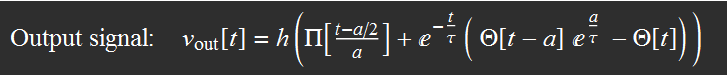



Square wave signal

The above result is just for one square pulse of duration a and RC time constant tau. We also need to simulate for square wave input. This can be done as follow.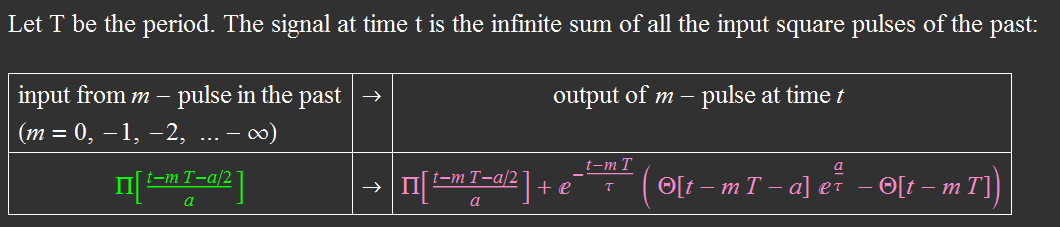




We can perform the sum as follow: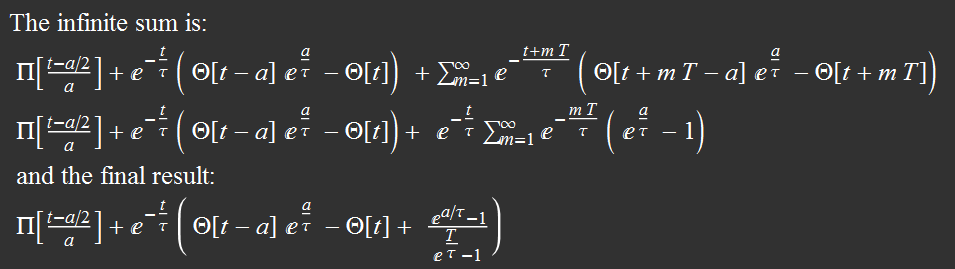




The above result is for one period t from 0 to T. Modulo function can be used to plot for any number of periods.

Results for differentiation circuit

We can obtain similar results for differentiation circuit.

For one square pulse: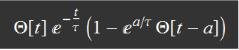



For a square wave, the function for one period t from 0 to T is: