Important: Digilent AD2 - a note

 Please go to update pages for the latest modification, class-wise issues, and others if links for those pages exist.
update page a  update page b   update page c

Lab work modification: - Do Part 0 ( Introduction), Part 1 (Instrumentation), and Part A only (three parts total): do everything, including answering/discussion all questions. - Experimental work of Part B and C are not required: It means no circuit, no measurement needs be done. You are required to only observe and write a report of your understanding, thoughts, and summary of these Parts. This should be put at the end of your report, a synthesis of everything that you learn in Lab 4. Create a subsection, titled "Report on observation of Parts B and C demonstrations". Do not mix this with what you summarize for your work in Part A. However, if you do any work along the line of Part B and Part C, you are welcome to include for extra credit.

Outcomes:

• You will demonstrate a simple signal amplifier and an optical sensor that can be used for many applications, such as remote control, robotics, or general-purpose light-level sensing
  

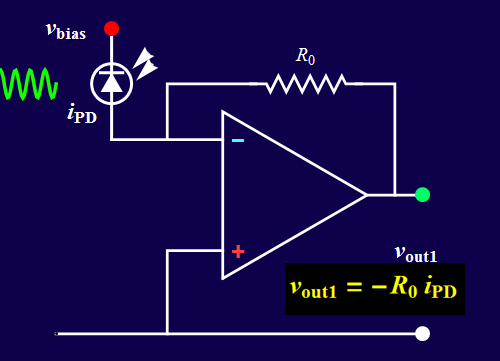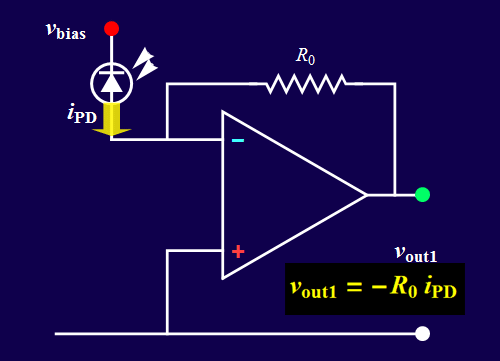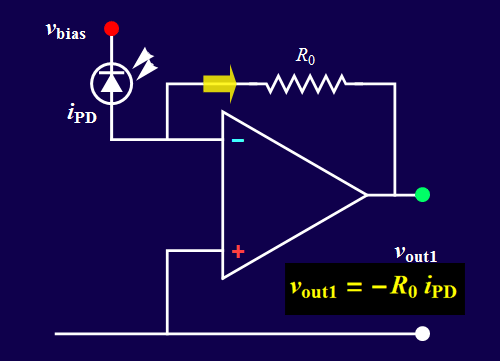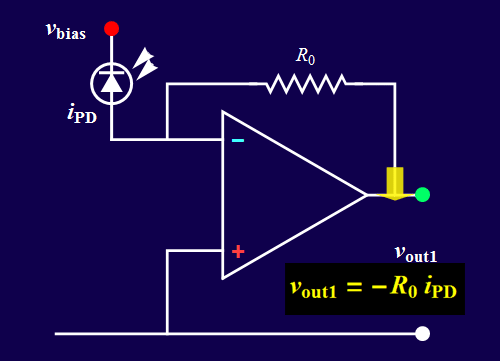
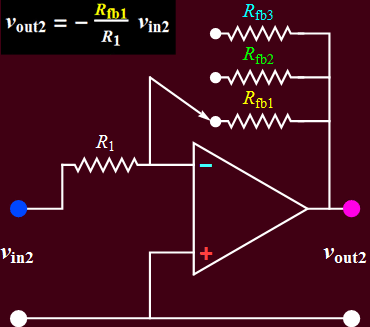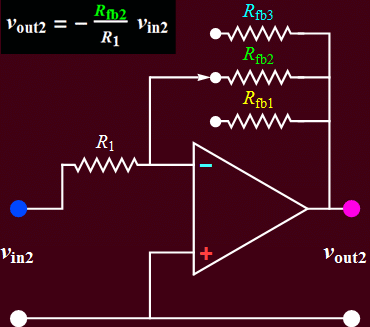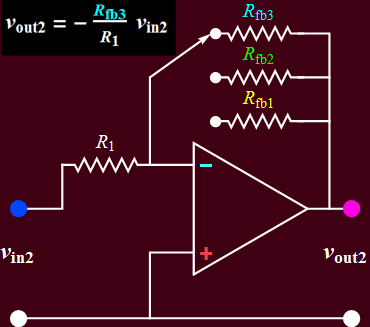
• You will build the circuits below. Circuit B is a voltage amplifier that accepts an input voltage signal and yields a proportional voltage output.  Circuit A converts the input current from a photodiode (a light sensor) into a proportional voltage output. It is also known as a transimpedance amplifier.

• Circuit B will be built first and tested. Once it is shown to function as intended, circuit A output will be the input of circuit B to make an optical sensor/receiver.
  

Circuit A	Circuit B

Both Circuit A and B joined together to form a single device: optical receiver (detector)

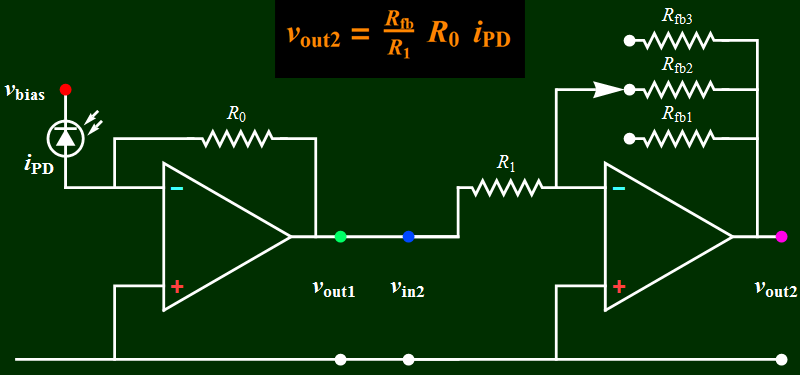For an optical sensor, the gain on B is adjusted to the light signal level. Low gain for strong signal, such as the light from a modulated LED placed near the diode. High gain for low light level such as scattered room light through an opening on the cover of a shielded diode. A remote control can be tested from a distance and high gain can be used to test the optical detector sensitivity.

Objectives:

You will learn and experiment with dependent sources, using operational amplifier - or “op amp” for short. Specifically, the op amp will be used as a dependent voltage source of which the output depends on:

a. an input AC voltage signal from an instrument (a signal generator), or a sensor (the photodiode of circuit A); this is the case for circuit B; or

b. an input current signal source which is from a photodiode; this is the case for circuit A

Introduction and background:

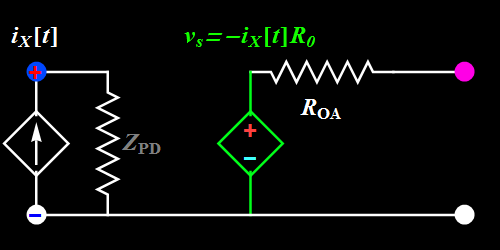
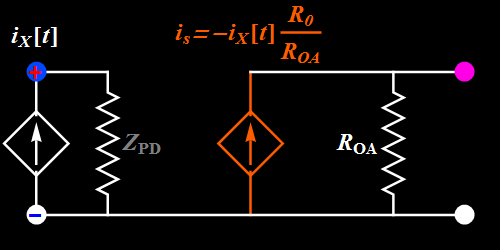
Please review your ECE2202 lecture as necessary on op amp and various op-amp circuits (note: This course is a lab course, hence we do not have time to go through the detailed circuit theory background. This page provides the minimum information you need to do the lab). The only knowledge that you need for this lab is the equivalent linear circuit models shown below.

Circuit A Note that the time-varying nature of the input signal current is explicitly shown as a function of time.	Circuit B Note that the time-varying nature of the input signal voltage is explicitly shown as a function of time.
Thevenin equivalent circuit	Thevenin equivalent circuit
Norton equivalent circuit	Norton equivalent circuit

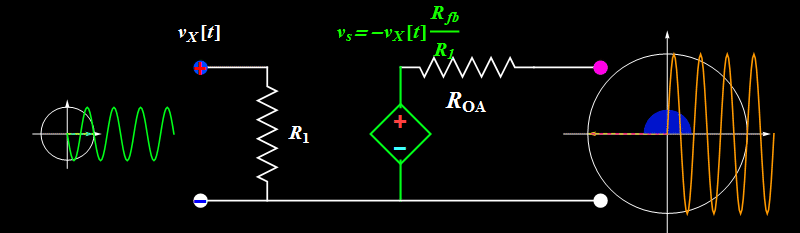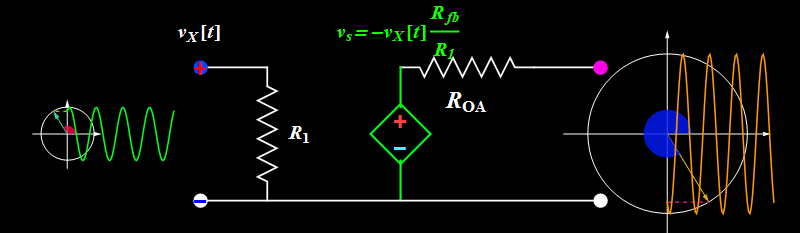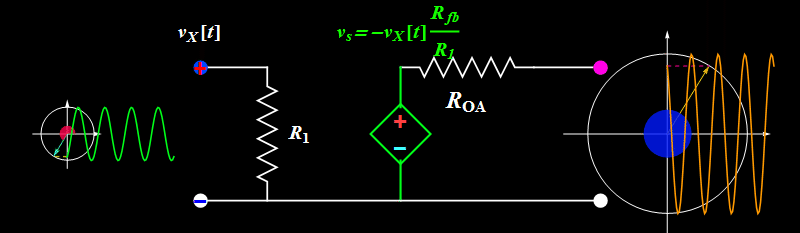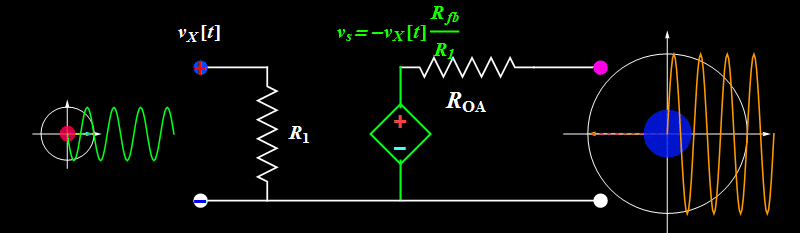
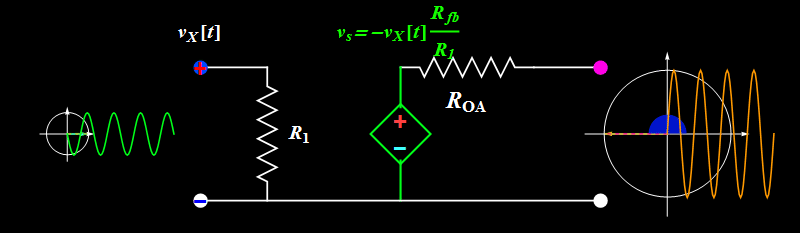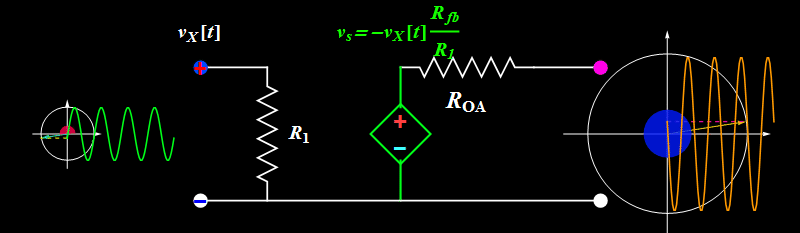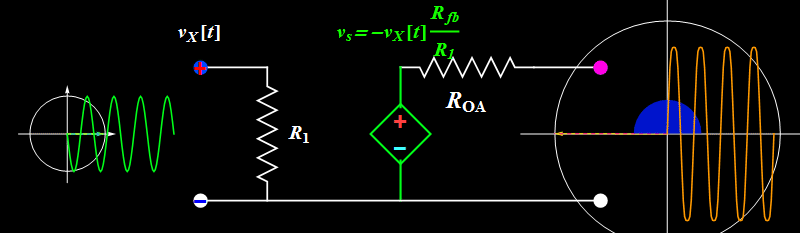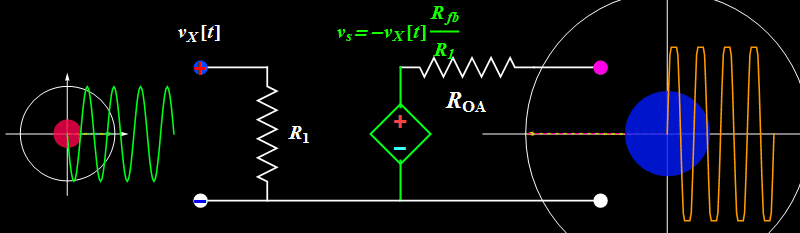
Let's take a look at Circuit B. How does it work?

Basic illustration

The left hand side shows a sinusoidal signal input. The right hand side shows the output from the dependent source. The output signal looks every way like the input except for the amplitude. Here, it is larger and we call it "amplification". If it is smaller, we would call it "attenuation". However, we can use the concept of amplification for both cases. We define that gain or amplification factor as the ratio of the output amplitude relative to that of the input. This includes both real amplification and attenuation.

So far so good. However, does the circuit truly work like the ideal formula above? We can find out by increasing the input signal amplitude.

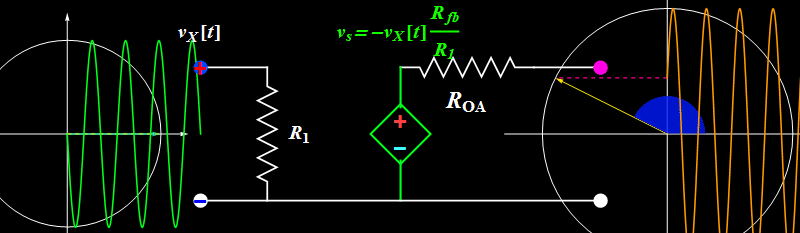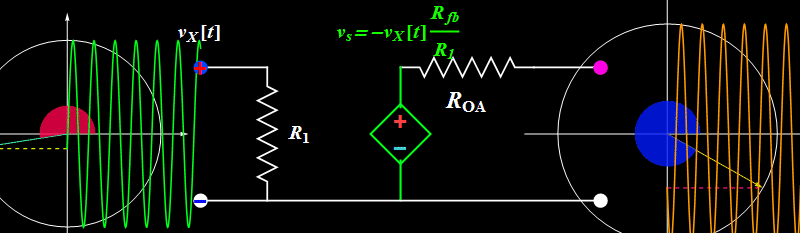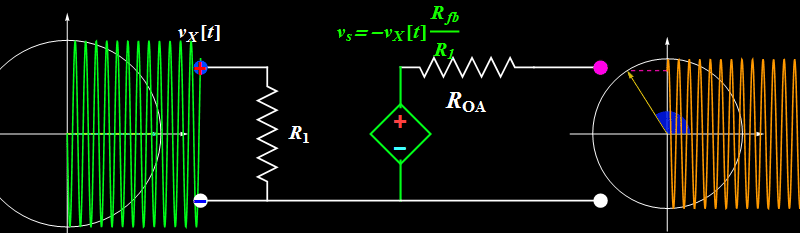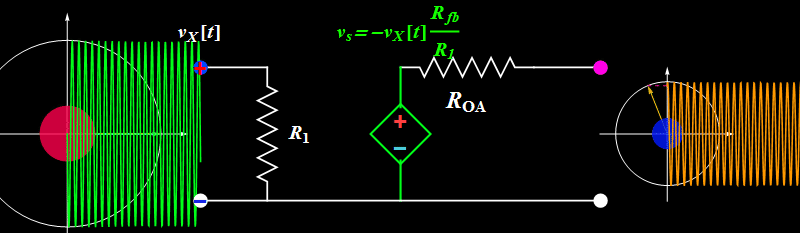
Topic 1: Amplitude saturation

At first, the circuit works as expected. We increase the input signal amplitude and the output amplitude increases proportionally. But does it increase without limit? There is no such a thing as infinite amplitude. Every source has finite amplitude and for our op-amp voltage amplifier, as it is biased with +- 15 V, we hit the ceiling when the output reaches those values. This is known as amplitude saturation.

A sinusoidal or any periodic signal has three parameters: amplitude, frequency, and phase. The above illustrates the amplitude effect. What about frequency and phase?

Topic 2: Bandwidth

Observe what happens to the output signal relative to the input as the frequency is changed. The animation above stops at every frequency change so that you can observe the phase relationship between the input and output. Also. what about the amplitude? Although the input amplitude is constant, the output amplitude changes vs frequency.

To get a clue what happens, consider the video below, go to the last part of video (0:53, above resonance) when the oscillation amplitude becomes quite small at high driving frequency. (You should watch the entire 1:07 video as well to learn about forced (or driven) oscillator - in Lab VI, we will build a circuit that can also have a resonance like the one in the video). Here, we don't have a resonance, but we have a "knee" or a "finite bandwidth". As the frequency goes higher than the op amp bandwidth, the op amp can't follow the rapidly oscillating signal, and its output amplitude drops.

https://www.youtube.com/watch?v=aZNnwQ8HJHU






Imagine we use this to amplify our music. Suppose its bandwidth is below the 44-kHz bandwidth for high-quality music, do you think the amplifier has high fidelity? (This is where the term "hifi" comes from).


If we use a square wave input at high frequency, are we sure we get exactly similar-looking square wave out?

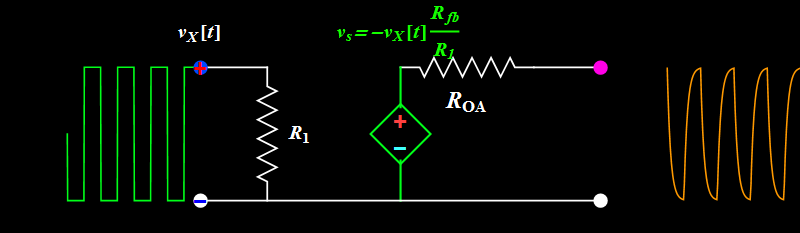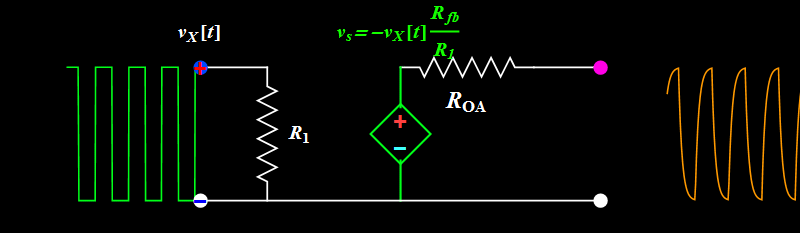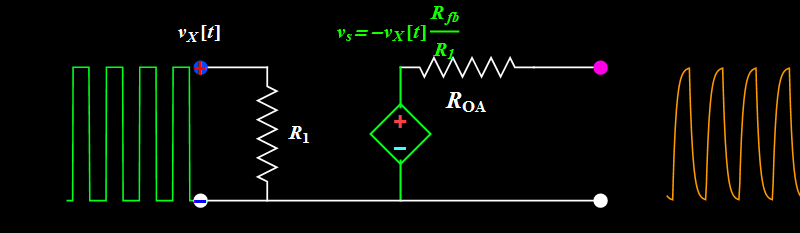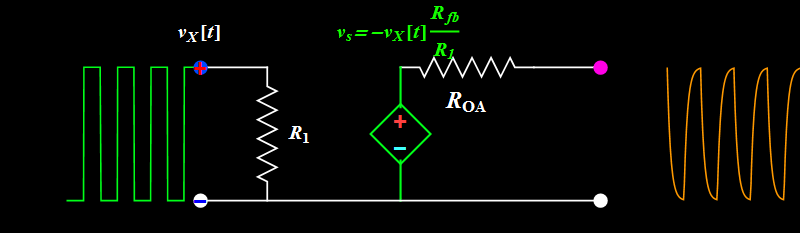Observe what happens to the sharp rising or falling edge of the square wave. The output doesn't seem to follow instantaneously, but is delayed in response. This time delay is always there even at low frequency, but if it is too small compared to the period, we just don't notice. At high frequency when the time delay is not negligible to a period, we see waveform distortion. What is the implication on signal fidelity?

Continue to page 2